Flächen und Flächenberechnung
Flächeninhalt, Umfang, Radius? Wir erklären dir im Folgenden, wie du all das im Handumdrehen für die verschiedensten geometrischen Formen berechnest.
Quadrat
Die einfachste Berechnung hast du beim Quadrat. Für die Fläche multiplizierst du eine Seite mit sich selbst. Für den Umfang nimmst du eine Seite mal vier.
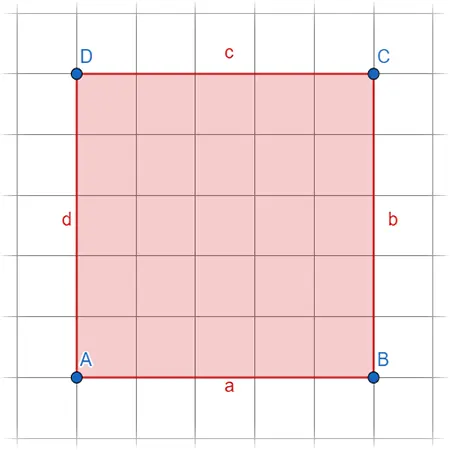
Flächeninhalt
\(A=a*a\)
Umfang
\(U=4*a\)
Rechteck
Der Flächeninhalt eines Rechtecks wird berechnet, indem du die lange Seite mit der kurzen Seite multiplizierst. Der Umfang errechnet sich durch 2 mal die lange Seite plus zwei mal die kurze Seite.
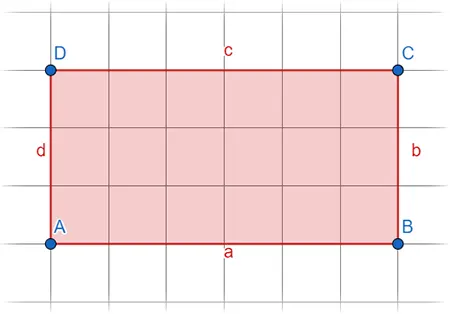
Flächeninhalt
\(A=a*b\)
Umfang
\(U=2*a + 2*b = 2*(a+b)\)
Kreis
Für die Berechnungen im Kreis benötigen wir die Kreiszahl \(\pi\). Sie ist eine Konstante, in jedem üblichen Taschenrechner eingespeichert und beträg ~3.1415.
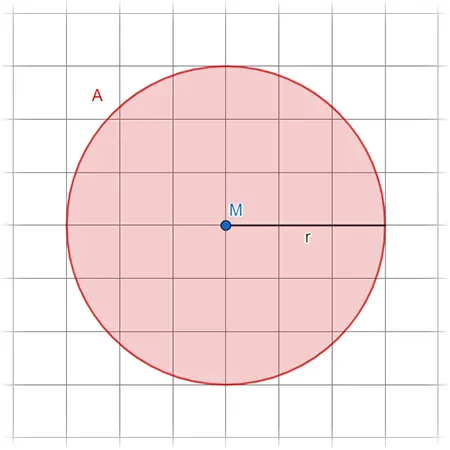
Flächeninhalt
\(A=\pi * r^2\)
Umfang
\(U=2 * \pi * r\)
Dreieck
Um die Fläche im Dreieck zu berechnen, brauchen wir die Höhe. Diese ist immer senkrecht auf der Grundseite, wobei ihr jede Seite als Grundseite hernehmen könnt. Der Umfang ist die Summe aller Seiten.
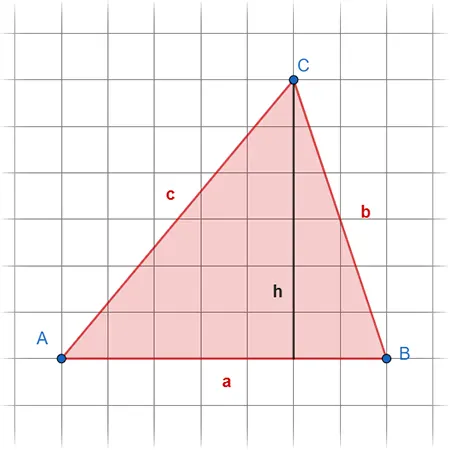
Flächeninhalt
\(A=0.5 * c * h\)
Umfang
\(U=a+b+c\)
Trapez
Die Fläche im Trapez berechnen wir, indem wir zuerst zwei parallel zueinander liegende Seiten addieren, und diese dann mal die Höhe und einhalb nehmen. Die Höhe muss senkrecht auf der parallelen Seite stehen. Der Umfang ist die Summe aller einzelnen Seiten.
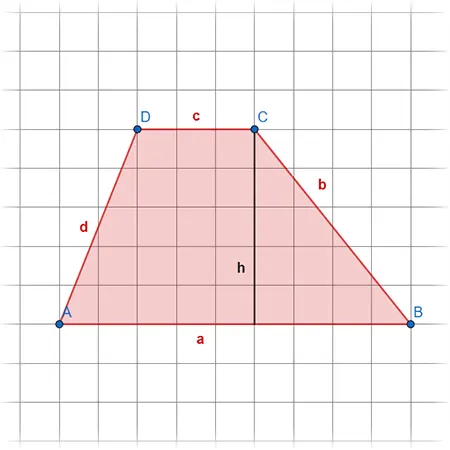
Flächeninhalt
\(A= 0.5 * (c+a) * h\)
Umfang
\(U= a+b+c+d\)
Parallelogramm
Die Berechnung des Flächeninhalts im Parallelogramm ist ähnlich zum Dreieck: Grundseite mal Höhe. Die Wahl der Grundseite ist nicht relevant, allerdings muss h senkrecht auf der Seite stehen. Der Umfang ist identisch zum Rechteck.
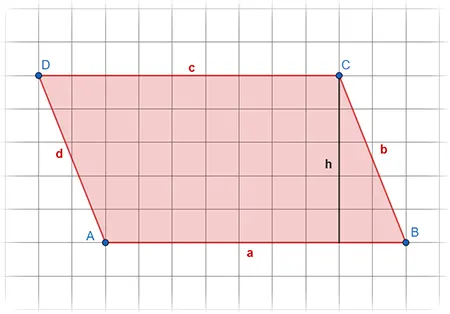
Flächeninhalt
\(A= a*h\)
Umfang
\(U= 2*a + 2*b =2*(a+b)\)
Drachenviereck
Den Flächeninhalt im Drachendreieck berechnen wir, indem wir die beiden Diagonalen mal nehmen und das dann halbieren. Der Umfang ist identisch zum Rechteck.
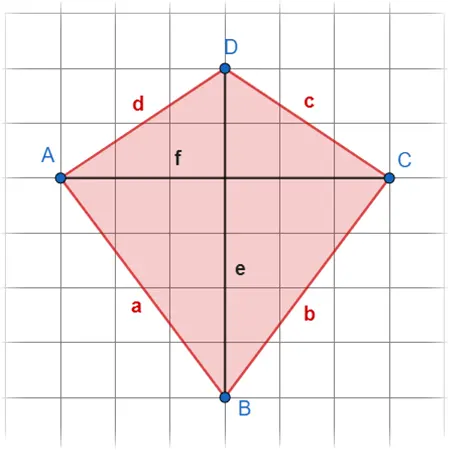
Flächeninhalt
\(A= 0.5 * e * f\)
Umfang
\(U= 2*a+2*b=2*(a+b)\)