Der Satz des Pythagoras - einfach erklärt
Der Satz des Pythagoras: Im rechtwinkligen Dreieck ist die Summe der Katheten Quadrate gleich dem Hypotenusen Quadrat.
Das Dreieck
Um die Seitenlängen berechnen zu können, müssen wir erst sichergehen, dass wir in einem rechtwinkligen Dreieck sind, das heißt ein Winkel muss 90° haben.
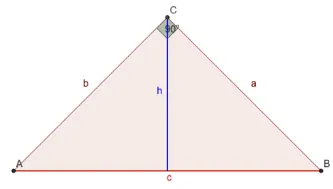
Hier ist der rechte Winkel oben am C.
Die Seiten
Als nächstes benennen wir die Seitenlängen. In diesem Fall ist c die Hypotenuse, da sie die längste Seite ist und gegenüber des rechten Winkels liegt.
Somit sind a und b die Katheten, also die beiden kleineren Seiten, die den 90° Winkel bilden.
Die Formel
Der Satz des Pythagoras: \(a^2+b^2=c^2\)
Oder auch: (Kathete)² + (Kathete)² = (Hypotenuse)²
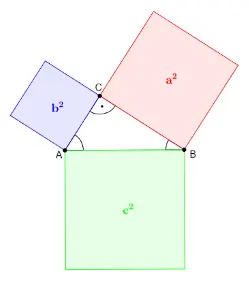
Und jetzt können wir das „hoch 2“ oder „Quadrat“ auch wörtlich nehmen, denn wie man in der Abbildung sehen kann addiert man die Quadrate der Katheten (rot + blau) und erhält das Hypotenusen Quadrat (grün).
Umstellen
Oftmals ist aber nicht die Suche nach der Seite c, manchmal muss man auch a oder b ausrechnen. Dafür stellen wir den Satz des Pythagoras ganz einfach um.
\(a^2=c^2-c^2\)
\(b^2=c^2-a^2\)
Beispiel
Nicht nur in der Schule kann die Formel wichtig sein. Hier ist ein Beispiel aus dem Alltag:
Ein Bauarbeiter hat eine 15 m lange Leiter und muss auf ein Hausdach kommen, das 12 m hoch ist. Wie weit vom Haus entfernt muss der Bauarbeiter die Leiter aufstellen?
1. Skizze erstellen und beschriften
a wird gesucht
b ist die Wand
c ist die Leiter
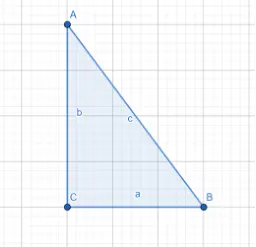
2. Was wissen wir?
a wird gesucht
b = 12 (die Hauswand)
c = 15 (die Leiter)
3. Formel aufstellen
\(a^2+b^2=c^2\)
4. Werte einsetzen und ausrechnen
\(a^2=15^2-12^2\)
\(a=\sqrt{15^2-12^2}\)
\(a=9\)
5. Ergebnis
Der Bauarbeiter muss die Leiter 9 m vom Haus entfernt aufstellen, um auf das Dach zu gelangen.